| 我国技术创新对就业弹性影响的实证分析 |
| 李从容,祝翠华 2009-03-19 |
| 摘 要: |
技术创新是产业结构优化、经济发展方式转变的核心。就业是我国最大的民生问题。从定量的角度研究技术创新对就业弹性的影响问题具有重要的现实意义。本文在理论分析的基础上,通过假设建立了技术创新对就业弹性的影响模型,然后将通过回归分析探讨了技术创新对就业弹性影响的作用机理,最后得出在中国经济高速增长的情况下,促进就业、提高就业弹性的重要途径是通过技术创新转变经济发展方式,促进产业结构优化,创造新行业。 |
| 关键词: |
技术创新,就业弹性,实证分析 |
|
|
为了保持经济长期平稳较快发展,缓解资源约束矛盾,走科学发展之路,党的十七大报告再次强调把增强自主创新能力作为国家发展战略。而随着我国经济高速发展和科技进步,我国就业压力却越来越大。据统计,2006年底,全国城镇登记失业人数为847万人,比上,年底增加8万人;城镇登记失业率为4.1%(2006年劳动保障统计数据快报)。这是否表明就业和自主创新、产业结构优化之间,存在着不可调和的矛盾?关于技术创新对就业影响的问题已成为理论界关注的热点问题。
西方理论界对技术创新与就业的关系问题已经形成了较为完善的分析框架,大名数的学者认为,在发达的市场经济条件下,技术创新短期会使失业增加,但从长期来看又可以创造新的就业岗位(毕先萍,李正友,2004)。我国学者基本上形成了两种观点:一种认为技术创新和资本深化,加剧了失业压力(姚战琪,夏杰长,2005);另一种观点认为,就中国的国情和经济增长轨迹而言,技术进步还不足以解释我国GDP就业弹性的下降(杨淑华,2007)。
从以上研究成果可以看出,理论界对技术创新与就业关系的探讨只是局限于整体分析,并未澄清技术创新与就业的作用机理,并且在对就业进行分析的过程中只选择了就业总量或者就业结构的绝对数,而没有分析技术创新对就业弹性的影响。因此,本文通过建立技术创新对就业弹性影响的分析模型,进一步探讨我国促进就业弹性提高的实现路径。
一、技术创新对就业弹性的分析模型
从古典经济学家开始,经济学家们就对技术创新与就业之间的关系进行了广泛的争论。相关研究最早可以追溯到古典经济学时期,以李嘉图为代表的古典经济学家认为,技术创新是一把"双刃剑",它在促进就业增加的同时,也会造成结构性失业。迄今为止,争论主要集中于技术创新对就业的综合影响上:一种观点认为技术创新对就业的影响以直接的破坏为主,导致了"技术性失业"(Clower,R.W.,1965;Malinvaud,E.,1977;Fabien PostelVinay,2002;Zagler,2002);另一种观点认为技术创新在直接破坏就业的同时,通过各种途径能够间接促进就业增加,因而总体上促进就业增长(OECD,1996;Clas Erlkson,1997;Pianta和Vivarelli,2001;BharatTrehan,2003)。
在发展经济学的理论中,希克斯按照要素间的边际替代率,将技术创新分为劳动节约型、资本节约型和中性型(谭崇台,2001)。他认为,劳动节约型技术创新,短期会导致用资本代替劳动,但是长期会对就业产生拉动效应。拉动就业效应产生主要基于以下的情况。(1)劳动需求减少的压力同时又成为提高劳动供给质量的动力,从而带来高技能劳动者就业。(2)劳动生产率提高、生产成本下降和产品价格水平降低,又可以扩大生产规模,扩大销售规模,进而增加对劳动力的需求,即"第二次就业效应"。不过,这一效应具有相对性,要受到产品需求弹性和行业竞争程度的制约。(3)对就业的间接影响,即技术创新开发新产品,开辟新的生产服务领域和新的产业,从而创造新的就业岗位。即"补偿就业效应"(蒋选,2000)。资本节约型技术创新对就业有短期促进作用,但是经过长期要素的价格调整又会增加资本而减少劳动。虽然节约资本型技术创新具有缓解资本紧张和就业压力的双重效应,但从宏观、动态、长期的意义来看,却不可能推动经济持续增长。
因此,假设技术创新短期减少就业,但长期可以带来新的就业机会,从而促进就业弹性的提高。具体模型如下式所示,IN表示技术创新:
EM=α+β2IN
二、模型指标选择
对模型进行实证检验,需要确定模型中变量的具体指标和数据来源,本文选择的具体指标及其解释如下:
(一)就业弹性指标
对一般社会现象而言,指标数据通常按月度、季度、年度分时段观察取得,但在短时间内微小变化难以观察和取得结果。因此,现实可行的弹性计算往往用差分公式。一般测算经济增长的就业弹性也使用差分公式,即经济增长的就业弹性EM=GL/GY,其中,GY表示经济增长速度,GL表示劳动投入的增长速度。
(二)技术创新指标
技术创新过程是一个知识创造、流动、应用和扩散的过程,从具体时间而言很难进行测度。但是人们为更好地了解创新能力和创新绩效,就采用黑箱的方法而忽略创新过程,延续生产函数的传统,从创新的投入和产出两端测量技术创新。技术创新投入的指标包括R&D经费支出和R&D活动人员投入;产出指标包括论文、专利、技术市场成交额和新产品产值等,其中专利是核心指标。大量的经验研究表明,论文、技术市场成交额等指标与专利的相关陸较高,所以通常采用专利作为技术创新的衡量指标,这里选择专利授权量和发明专利授权量作为产出指标。技术创新具体指标包括R&D经费支出(亿元)(R&DC)、R&D活动人员全时当量(万人年)(R&DP)、专利授权量(件)(Pa)、发明专利授权量(件)(IPa)(刘凤朝,孙玉涛,2008)。
三、模型计量结果分析
本研究采用1992-2006年中国就业弹性、经济、技术创新和产业结构的相关数据(参考各年的《中国统计年鉴》),运用spss16.0实证分析。在实证分析之前,考虑到原始数据的单位和量级存在较大的差异,为了避免数据中其他因素的干扰,保证数据的平稳性,这里对原始数据进行取对数处理。模型实证具体结果如表一l所示。
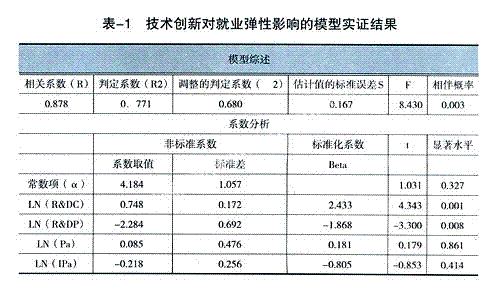
(一)拟合优度检验
数据处理结果中,相关系数R=0878,判定系数R2=0.771,调整的判定系数(2)=0.680,因此可以判断技术创新对就业弹性影响的线性回归的拟合程度相对较好。
(二)回归方程的显著性检验(F检验)
从结果来看,回归估计的标准误差S=0.167,F=8.430,临界值Fα=3.41,F>Fα,相伴概率值p=0.003,p<0.05,这说明所有技术创新对就业弹性影响的线性回归系数同时与零有显著差异,技术创新的各变量与就业弹性之间存在显著线性关系。
(三)回归系数的显著性检验(t检验)
LN(R&DC)系数的-t-=4.343,临界值tα=2.160,-t->tα,相伴概率值p=0.001,p<0.05,这说明LN(R&D/GDP)与就业弹性之间存在显著的线性关系。
LN(R&DP)系数的-t-=3.300,临界值tα=2.160,-t-tα,相伴概率值p=0.008,p<0.05,这说明LN(AGDP)与就业弹性之间存在显著的线性关系。
LN(Pa)、LN(IPa)系数的-t-<tα,p>0.05,因此这两项与就业弹性没有相关关系,应在回归方程中被剔除。
从以上的分析来看,技术创新在我国的就业溢出效应还不明显,还处于技术创新对就业的短期替代作用。但是也应当看到技术创新的投人与就业弹性的增长正在呈同向变化,虽然变动幅度比较小,然而笔者相信达到某一拐点之后技术创新会带来明显的就业效应。
四、结论及政策建议
通过以上分析,可以得出结论:技术创新对就业的拉动作用已开始显现。从实证结果中可以得出,技术创新的投入对就业弹性存在正向的促进作用,虽然这种作用比较小,但是技术创新创造就业的特点开始显现。这一点也正验证了学术界大多数学者的观点,即在发达的市场经济条件下,技术创新短期会使失业增加,但从长期来看又可以创造新的就业岗位。
因此,在中国经济高速增长的情况下,促进就业、提高就业弹性的重要途径是通过技术创新转变经济发展方式,促进产业结构优化,创造新行业。相应的对策建议为:首先,通过技术创新,把依赖人力、资本和能源投入的外延式发展,转变为依赖知识和技术的内涵式发展;其次,大力发展高新技术产业、现代服务业等知识密集型产业,通过高新技术改造传统产业,促进产业升级和优化;最后,大力扶植和鼓励企业技术创新,要加大和鼓励对研究开发的投资,通过技术创新,提高劳动者的人力资本,同时通过产业结构的调整,创造山新的产业,扩大就业领域。
|
|
|

